GCD of Two Numbers - Euclidean Algorithm

Brute force Approach to find GCD of Two numbers:

In this approach we first check if both a and b have the value 0. If yes, the GCD(a,b) is not defined.
If not we check if either of a and b is 0. In this case the non-zero number among a and b is the GCD(a,b).
If the values of both a and b is not 0, we check for all numbers from 1 to min(a,b) and find the largest number which divides both a and b. This largest number which divides both a and b is said to be the GCD(a,b).

EXAMPLE:

let a=5 b=10
min(a,b)=min(5,10)=5
numbers between 1 to 5 are 1,2,3,4,5
The highest number which divides both 5 and 10 is 5
So, GCD(5,10)=5

Time Complexity : O(min(a,b))
Space Complexity : O(1)

C++ Program for Brute force GCD:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int a,b,mi,gcd,i;
    cout << "Enter the values of a and b" << endl;
    cin >> a >> b; // Taking a and b as input
    if(a==0 && b==0) // checking if the values of both a and b are 0
    {
        cout << "GCD is not defined" << endl;
    }
    else if(a==0) // checking if the value of a is 0
    {
        cout << "GCD of " << a << " and " << b << " is " << b << endl;
    }
    else if(b==0) // checking if the value of b is 0
    {
        cout << "GCD of " << a << " and " << b << " is " << a << endl;
    }
    else
    {
        mi=min(a,b); // finding the min of a and b
        for(i=1;i<=mi;i++) // loop to check numbers from 1 to mi(a,b)
        {
            if(a%i==0 && b%i==0) //checking if i is divisible by both a and b
            {
                gcd=i; // if yes, updating the value of gcd with i
            }
        }
        cout << "GCD of " << a << " and " << b << " is " << gcd << endl;
    }
    return 0;
}

 TESTCASE:

Enter the values of a and b
37 55
GCD of 37 and 55 is 1

Euclidean Algorithm to find GCD of Two numbers:

If we recall the process we used in our childhood to find out the GCD of two numbers, it is something like this:

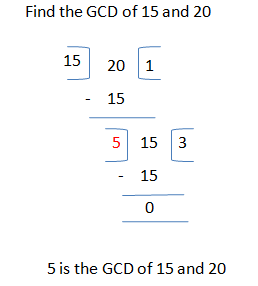
This process is known as Euclidean algorithm.
The idea behind this algorithm is,
GCD(a,b) = GCD(b,r₀)   where, a = bq₀ + r₀ and a>b
GCD(b,r₀) = GCD(r₀,r₁)  where, b = r₀q₁ + r₁ and b>r₀
GCD(r₀,r₁) = GCD(r₁,r₂)   where, r₀= r₁q2 + r₂ and r₀>r₁
.
.
GCD(r_i-1,r_i) = GCD(r_i,0)   where, r_i-1 = r_iq_i+1 + 0 and r_i-1>r_i
GCD(r_i,0) = r_i   (Since, GCD(k,0) = k and k != 0)

Why is GCD(a,b) = GCD(b,r₀) ?

Let g = GCD(b,r₀)
r₀ = g*c₁ 
b = g*c₂
a = bq₀+r₀
a = (g*c₂)q₀ + (g*c₁)
a = g * (c₂q₀ + c₁)
So we can say that g is also the GCD(a,b)   (Since, c₁=1 or c₂ and c₁ do not have any common factors)
therefore, GCD(a,b) = GCD(b,r₀)

EXAMPLE:

Let a=32 b=10
GCD(32,10) = GCD(10,5)   [32=10(3)+2]
GCD(10,5) = GCD(2,0)       [10=2(5)+0]
GCD(2,0) = 2
So, GCD(32,10) = 2

Time Complexity : O(log(min(a,b)))
Space Complexity : O(1)

C++ program for GCD using Euclidean Algorithm:

#include<bits/stdc++.h>
using namespace std;
int find_gcd(int a,int b);
int main()
{
    int a,b,gcd;
    cout << "Enter the values of a and b" << endl;
    cin >> a >> b; // Taking a and b as input
    if(a==0 && b==0) // checking if the values of both a and b are 0
    {
        cout << "GCD is not defined" << endl;
    }
    else
    {
        gcd=find_gcd(a,b); // calling the function to find gcd of a and b
        cout << "GCD of " << a << " and " << b << " is " << gcd << endl;
    }
    return 0;
}
int find_gcd(int a,int b) // reccursive function to find gcd of a and b
{
    if(a==0) // cheching if value of a is 0
    return b; // if yes, returning the value b
    else if(b==0) // cheching if value of b is 0
    return a; // if yes, returning the value a
    else if(a==b) // checking if the value of a and b is equal
    {
        return a; // if yes, returning gcd=a=b
    }
    else
    {
        if(a>b) // checking if a is greater than b
        {
            return find_gcd(b,a%b); // if yes, returning the gcd of b and reminder of a when divided by b
        }
        else
        {
            return find_gcd(a,b%a); // if no, returning the gcd of a and reminder of b when divided by a
        }
    }
}

 TESTCASE:

Enter the values of a and b
56 24
GCD of 56 and 24 is 8