Moore's Voting Algorithm: Given an integer array of length N. Check if there exists an integer which occurs more than floor(N/2) times. If there is no such element, print THERE IS NO MAJORITY ELEMENT.
Before going into the algorithm, let us see something interesting.
Let,
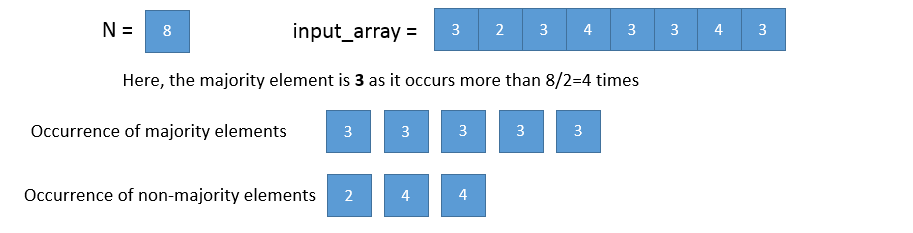
Let us eliminate two distinct numbers from the array. For this there are two possibilities :
Case 1: One number lies in majority elements and the other number lies in non-majority elements.
Case 2: Both the numbers lie in non-majority elements.
However, the occurrence of the majority elements contains the same number. So it is not possible to remove two distinct numbers from the occurrence of majority elements.
Case 1: One number lies in majority elements and the other number lies in non-majority elements.

After removing the elements, the majority element is still 3 as it occurs more than 6/2=3 times.
Therefore, there is no change in the majority element in this case.
Case 2: Both the numbers lie in non-majority elements.

After removing the elements, the majority element is still 3 as it occurs more than 6/2=3 times.
Therefore, there is no change in the majority element in this case.
The same idea is used in Moore’s Voting algorithm.
For this, we use two variables majority_element and count.
majority_element stores the majority element upto that instance and count stores its frequency upto that instance.
Initially, majority_element = input_array[0] and count = 1. Because input_array[0] has occurred once till this instance.
Now we traverse through the remaining elements. While traversing, if the array element is the same as the majority_element, we increment count by 1. If not, we decrement count by 1.
If count becomes 0 at any instance, we change the majority_element to the input_array element accessed at that instance and change count to 1.
The majority_element which we obtain after traversing all the input_array elements is expected to be the majority element of the complete array.
To find out if the element is actually the majority_element, we need to traverse again through all the input_array elements and count the frequency of majority_element in the array. If the frequency of the majority_element is greater than N/2, it is said to be the majority element.
If not, there is no majority element in the input_array.
Example:

Initially,
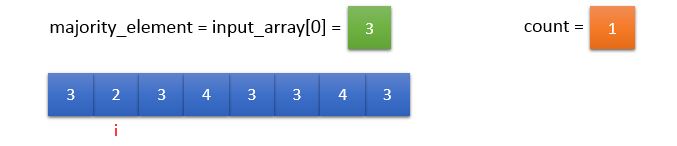
input_array[i] != majority_element. So, count should be decremented by 1.
Since count = 0, majority_element = input_array[i] and count = 1.
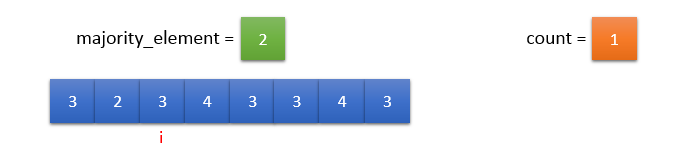
input_array[i] != majority_element. So, count should be decremented by 1.

Since count = 0, majority_element = input_array[i] and count = 1.
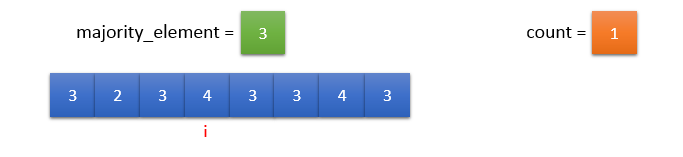
input_array[i] != majority_element. So, count should be decremented by 1.

Since count = 0, majority_element = input_array[i] and count = 1.
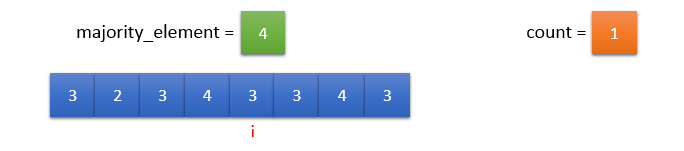
input_array[i] != majority_element. So, count should be decremented by 1.

Since count = 0, majority_element = input_array[i] and count = 1.
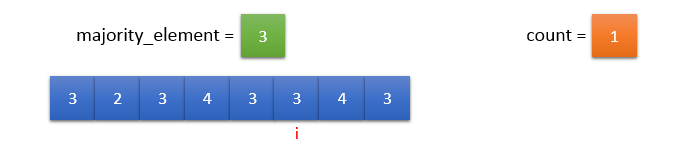
input_array[i] == majority_element. So, count should be incremented by 1.
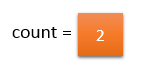
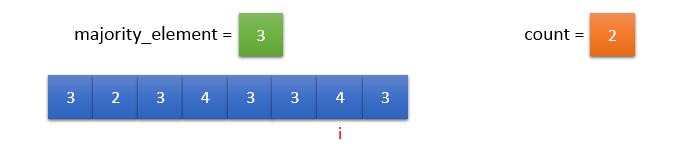
input_array[i] != majority_element. So, count should be decremented by 1.
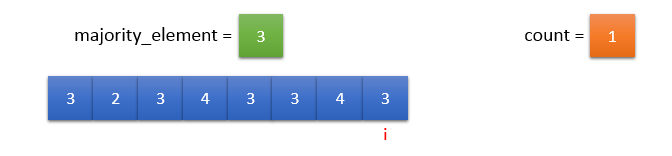
input_array[i] == majority_element. So, count should be incremented by 1.
After traversing all the elements,

Now lets count the occurrence of majority_element in input_array.


Time Complexity: O(n)
Space Complexity: O(1)
Let us See the Code for Moore's Voting Algorithm :
{tab title="C++" class="blue"}
/* This code is contributed by Tangudu Sai Kiran */
#include <bits/stdc++.h>
using namespace std;
void isMajorityElement(int N, int input_array[])
{
int majority_index=0,count=1;
for(int i=1;i<N;i++) //loop to find the possible majority element
{
if(input_array[majority_index]==input_array[i])
count++;
else
count--;
if(count==0)
{
majority_index=i;
count=1;
}
}
count=0;
for(int i=0;i<N;i++) //loop to find the frequency of majority element
{
if(input_array[majority_index]==input_array[i])
count++;
}
if(count>N/2) //checking for majority
cout<<"MAJORITY ELEMENT: "<< input_array[majority_index]<< endl;
else
cout<<"THERE IS NO MAJORITY ELEMENT"<<endl;
}
int main()
{
int input_array[]={2, 2, 3, 2, 4, 2, 5};
int N=sizeof(input_array)/sizeof(input_array[0]);
isMajorityElement(N, input_array); //calling isMajorityElement function
return 0;
}
{tab title="Java" class="red"}
/* This code is contributed by Tammisetti Naveen */
import java.util.*;
public class FindMajority
{
static void isMajorityElement(int N, int input_array[]) // function to check the majority element is occurring more than n/2 times
{
int count = 0;
int majority_element = MajorityElement(N, input_array);//Calling MajorityElement function to find the possible majority element
for (int i = 0; i < N; i++) // loop to find the frequency of possible majority element
{
if (input_array[i] == majority_element) // Checking if input_array[i] is equal to majority_element
count++; // if yes, increment count
}
if (count > N/2)
System.out.print ("MAJORITY ELEMENT: " + majority_element);
else
System.out.print ("THERE IS NO MAJORITY ELEMENT");
}
static int MajorityElement(int N, int input_array[]) // function to find the possible majority element
{
int majority_element = input_array[0], count = 1;
for(int i = 1; i < N; i++)
{
if (majority_element == input_array[i])
count++;
else
count--;
if (count == 0)
{
count = 1;
majority_element = input_array[i];
}
}
return majority_element;
}
public static void main(String[] args)
{
int input_array[] = {2, 2, 3, 2, 4, 2, 5};
int N = 7;
isMajorityElement(N,input_array);//calling isMajorityElement function
}
}
{tab title="Python" class="green"}
'''This code is contributed by Arun Reddy'''
def majorityElement(input_array,N):
majority_element=input_array[0]
count = 1
for i in range(1,N):
if input_array[i]==majority_element:
count+=1
else:
count-=1
if count==0:
count=1
majority_element=input_array[i]
count = 0
for i in input_array: #loop to count the occurence of majority_element
if i==majority_element:
count+=1
if count>N//2:
print("MAJORITY ELEMENT: ",majority_element)
else:
print("THERE IS NO MAJORITY ELEMENT")
if __name__=="__main__":
input_array=[2, 2, 3, 2, 4, 2, 5]
N=7
majorityElement(input_array,N) #calling majorityElement function
{/tabs}
OUTPUT:
MAJORITY ELEMENT: 2