Given an array of length N-1 with integers from 1 to N and one missing integer, we need to find the missing integer.
Note : No integer is repeated twice.
Approach 1 :
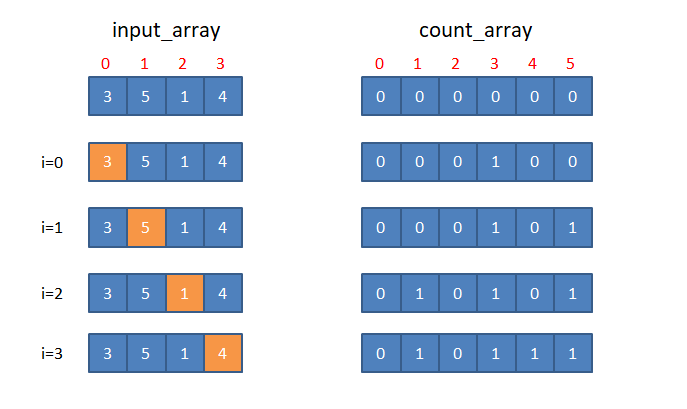
The idea of this approach is to store the frequency of each element of input_array in an other array say, count_array of length N+1. The indices of count_array correspond to the integers 1 to N. We iterate through each element in the input_array and increment the frequency of its corresponding index in count_array. After updating the frequency of all the elements, we find a position with value 0 between indices 1 and N (inclusive) in count_array. The index of this position gives the missing number.
EXAMPLE:
Let
N=5, andinput_arrayis {3,5,1,4}
Here,
count_array[2] = 0. So the missing number is 2.
Time complexity : O(N)
Space complexity : O(N)
LET US SEE THE CODE:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N,i;
cout << "Enter the value of N" << endl;
cin >> N; // Taking N as input
int input_array[N-1];
int count_array[N+1]={0}; // Array to count frequency
cout << "Enter array elements" << endl;
for(i=0;i<N-1;i++)
{
cin >> input_array[i]; // Taking input of ith element of input_array
count_array[input_array[i]]++; // Updating the frequency of input_array[i]
}
for(i=1;i<=N;i++)
{
if(count_array[i]==0) // Condition to check if the frequency is 0
{
cout << "Missing integer is " << i << endl;
break; // Once we find the missing element, there is no need to check for the remaining elements
}
}
return 0;
}
TESTCASE:
Enter the value of N 4 Enter array elements 3 2 1 4 Missing integer is 4
Approach 2 :
The idea of this approach is,

So we calculate the sum of all integers from 1 to N (inclusive) and sum of all elements in input_array and get their difference.
EXAMPLE:
Let
N=5, andinput_arrayis {3,5,1,4}
Sum of elements from1 to N= 1+2+3+4+5 = 15
Sum of elements ofinput_array= 3+5+1+4 = 13
Missing number = 15-13 = 2
Time complexity : O(N)
Space complexity : O(1)
LET US SEE THE CODE :
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N,i;
cout << "Enter the value of N" << endl;
cin >> N; // Taking N as input
int input_array[N-1];
int count_array[N+1]={0}; // Array to count frequency
int array_sum=0,integer_sum=0,missing_number;
cout << "Enter array elements" << endl;
for(i=0;i<N-1;i++)
{
cin >> input_array[i]; // Taking input of ith element of input_array
array_sum += input_array[i]; // Calculating sum of all elements in input_array
}
for(i=1;i<=N;i++)
{
integer_sum += i; // Calculating sum of all integers between 1 to N
}
missing_number = integer_sum - array_sum; // Calculating the missing number
cout << "Missing integer is " << missing_number << endl;
return 0;
}
TESTCASE:
Enter the value of N 5 Enter array elements 3 2 1 5 Missing integer is 4